Обнаружена в раскопках, так называемая, «вестоницкая кость» с зарубками. Позволяет историкам предположить, что уже тогда наши предки были знакомы с зачатками счета.

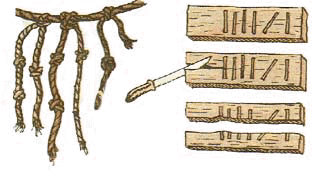
Кипу (khipu - исп. quipu — «узел», «завязывать узлы», «счёт») древняя мнемоническая и счётная система (в связке со счётным устройством юпаной) инков и их предшественников в Андах, своеобразная письменность: представляет собой сложные верёвочные сплетения и узелки, изготовленные из шерсти южноамериканских верблюдовых (альпаки и ламы) либо из хлопка. Узелковые носители информации «кипу», которыми инки пользовались вместо письменности, являются аналогом современного двоичного кода. К такому выводу пришел гарвардский исследователь древней южноамериканской цивилизации Гари Эртон. По утверждению Эртона узелки на шнурках, завязанные инками, представляют собой 7-битный двоичный код и могут передавать до 1500 отдельных знаков.

Согласно результатам исследований Эртона, у инков существовало семь способов завязывания «кипу». Общее число вариантов, полученных при сочетании различных методов вязания, достигает 128. Однако, как отмечает ученый, с учетом использования инками шнурков 24 цветов число комбинаций «кипу» достигает 1536.

Выводы Эртона говорят о том, что, применяя «кипу», инки по количеству возможных к передаче знаков превзошли шумеров с их приблизительно 1000-1500 информационными блоками и в два раза превысили количество иероглифов египтян и майя. Если выводы профессора найдут подтверждение, получится, что инки изобрели двоичный код, как минимум, за 500 лет до появления компьютера и использовали его в трехмерной письменности.

Юпана (yupana «счётное устройство») — разновидность абака, использовавшаяся в математике инков государства Тауантинсуйу. Существовало несколько разновидностей юпаны. Предполагалось, что вычисления на юпане осуществлялись на основе системы счисления с основанием 40, но некоторые исследователи склоняются к тому, что в юпане использовалась фибоначчиева система счисления, чтобы минимизировать необходимое для вычислений число зёрен.

На коленях статуи царя Гудеа - правителя древнего государства Лагаша в шумере, установлена доска, на которой вырезана масштабная линейка в половину локтя вавилонского царя. Линейка разделена на 16 равных частей, из которых вторая справа разделена на 6, четвертая - на 5, шестая-на 4, восьмая-на 3 и десятая-на 2 равные части. Наименьшие деления - около миллиметра.

Найденные части устройства

Антикитерский механизм - механическое устройство, обнаруженное в 1902 году на затонувшем античном судне недалеко от острова Антикитера. Датируется приблизительно 87 годом до н. э. Хранится в Национальном археологическом музее в Афинах.

Механизм содержит большое число бронзовых шестерён в деревянном корпусе, на котором размещены циферблаты со стрелками. Использовалось для расчёта движения небесных тел.  В нём применялась дифференциальная передача. Ранее считалось, что она была изобретена не раньше XVI века.

Полная схема устройства была восстановлена только в 1971 году .
 

Реконструированное устройство

Абак от лат. "аbacus", греч. "аbax" - доска.
Это первый прибор позиционного (поразрядного) счета. Появился в 5 в. до н.э. в странах Древнего Востока. В Грецию абак завезен финикийцами и стал там "походным инструментом" греческих купцов. В 1846 г. на острове Саламин в Эгейском море был найден единственный сохранившийся греческий абак - "саламинская плита", в виде мраморной доски 150х75 см.

Древнегреческий абак представлял собой посыпанную морским песком дощечку. На песке проходились бороздки, на которых камешками обозначались числа. Одна бороздка соответствовала единицам, другая - десяткам и т.д. Если в какой-то бороздке при счете набиралось более 10 камешков, их снимали и добавляли один камешек к следующему разряду.

Греческий абак (реконструкция), Политехнический музей, Москва

В результате длительной эволюции сложились три классические формы абака (китайские, японские и русские счеты), сохранившие свое значение до последнего времени.

Римляне усовершенствовали абак, перейдя от деревянных досок, песка и камешков к мраморным доскам с выточенными желобками и мраморными шариками.

http://www.joernluetjens.de/

В Китае счеты Суаньпань (суань-пан или суан-пан) - разновидность абака, конструкция сформировалась в Китае к 12 в., принцип счета основан на пятиричной системе. Предназначен для выполнения сложения и вычитания, умножение и деление чисел сводится к сложению и вычитанию. Согласно правилам работы косточки передвигаются к перегородке, при этом прибор располагается горизонтально, большой стороной с пятью косточками к вычислителю.

Суаньпань состояли из деревянной рамки, разделенной на верхние ("Небо") и нижние ("Земля") секции. Палочки соотносятся с колонками, а бусинки с числами.
Она разделена на две части: в нижней части на каждом ряду располагаются по 5 косточек, в верхней части - по две. Таким образом, для того чтобы выставить на этих счетах число 6, ставили сначала  косточку, соответствующую пятерке, и затем прибавляли одну в разряд единиц.

Суан-пан

http://www.joernluetjens.de/

Серобян

http://www.joernluetjens.de/

В Японии это же устройство для счета носило название серобян - разновидность абака, появился в 16 в. в результате эволюции китайского суаньпаня.

Серобян является cовременным вспомогательном средством для счета и учебное пособие в школах Японии. Способствует развитию устного счета, изучению десятичной системы счисления, помогает приобрести определенные навыки необходимые при работе на клавиатуре компьютера.

Счеты появились в допетровской Руси и прошли долгий путь развития - от "дощаного счета" 16 века с четырьмя счетными полями в двух складных ящичках до современных - в деревянной раме.

На Руси долгое время считали по косточкам, раскладываемым в кучки. Примерно с XV века получил распространение "дощаный счет", завезенный, видимо, западными купцами вместе с ворванью и текстилем. "Дощаный счет" почти не отличался от обычных счетов и представлял собой рамку с укрепленными горизонтальными веревочками, на которые были нанизаны просверленные сливовые или вишневые косточки.

Счёты, которые использовались в 19-20 вв

http://www.joernluetjens.de/

Конец V - начало IV в. до н. э. В произведениях древнегреческих поэтов Гомера и Аристофана упоминается о распространении пальцевого счета, зародившегося в древности и до сих пор употребляющегося в ряде случаев биржевыми маклерами.

Аристотель

Аристотель (384-322 гг.до н.э.) в своих книгах "Категории", "Первая аналитика", "Вторая аналитика" и др. подверг анализу человеческое мышление и его формы: понятия, суждения, умозаключения. В своих трудах Аристотель впервые обосновал один из важнейших разделов логики - учение о суждениях и силлогизмах.

Газета "ИНФОРМАТИКА" Аристотель, Лейбниц, Буль

Герон Александрийский создает технические автоматические устройства, описания которых дошли до наших дней: Его учитель Ктезибий Александрийский создал автоматические водяные часы (клепсидра).

На раскопках в 1964 году, было обнаружено, что индейцы майя имели кубики с календарными иероглифами, которые использовались ими в качестве особого типа счетных камешков.

Беда Достопочтенный.
Иллюстрация из Нюрнбергской хроники. XV в.

Один из первых математиков Европы англосаксонский математик Беда Достопочтенный (Bede Venerabilis, 672 или 773 - 27 мая 735 гг.) в своем трактате "О счислении" дал полное описание счета на пальцах до миллиона. Он писал:
"В мире есть много трудных вещей, но нет ничего труднее, чем четыре действия арифметики".

Французский монах Герберт из Орийяка (ставший позже папой римским Сильвестром II) написал книги по математике и среди них "Правила счета на абаке", где описывал абак в виде гладкой доски, посыпанной голубым песком и имеющей 30 столбцов, из которых 3 отводились дробям . Ему же приписывается первенство в создании механических часов.

Индийские ученые сделали одно из важнейших в математике открытий. Они изобрели позиционную систему счисления, которой теперь пользуется весь мир.

При записи числа, в котором отсутствует какой-либо разряд (например, 101 или 1204), индийцы вместо названия цифры говорили слово "пусто". При записи на месте "пустого" разряда ставили точку, а позднее рисовали кружок. Такой кружок назывался "сунья" - на языке хинди это означало "пустое место".

Арабские математики перевели это слово по смыслу на свой язык - они говорили "сифр". Современное слово "нуль" родилось сравнительно недавно - позднее, чем "цифра". Оно происходит от латинского слова "nihil" - "никакая".

Мухаммед бен Муса ал-Хорезм

Приблизительно в 850 году н.э. арабский ученый математик Мухаммед бен Муса ал-Хорезм (из города Хорезма на реке Аму-Дарья) написал книгу об общих правилах решения арифметических задач при помощи уравнений. Она называлась "Китаб ал-Джебр". Эта книга дала имя науке алгебре. Очень большую роль сыграла еще одна книга ал-Хорезми, в которой он подробно описал индийскую арифметику. Триста лет спустя (в 1120 году) эту книгу перевели на латинский язык, и она стала первым учебником "индийской" (то есть нашей современной) арифметики для всех европейских городов.

Мухаммеду бен Муса ал-Хорезму мы обязаны появлению термина "алгоритм".

Леонардо да Винчи

Леонардо да Винчи (Leonardo da Vinci, 16.04.1452-02.05.1519) создал  13-разрядное суммирующее устройство с десятизубными кольцами около 1500 года. 

Среди двухтомного собрания рукописей, известных как "Codex Madrid", посвященных механике, были обнаружены чертежи и описание такого устройства. Похожие рисунки также были найдены и в рукописях "Codex Atlanticus". 

Основу машины по описанию составляют стержни, на которые крепится два зубчатых колеса, большее с одной стороны стержня, а меньшее - с другой. Эти стержни должны были располагаться таким образом, чтобы меньшее колесо на одном стержне входило в зацепление с большим колесом на другом стержне. При этом меньшее колесо второго стержня сцеплялось с большим колесом третьего, и т.д. Десять оборотов первого колеса, по замыслу автора, должны были приводить к одному полному обороту второго, а десять оборотов второго - один оборот третьего и т.д. Вся система, состоящая из 13 стержней с зубчатыми колесами должна была приводиться в движение набором грузов. 

Рисунок этого устройства был обнаружен только в 1967 году, и по нему фирма IBM воссоздала вполне работоспособную 13-разрядную суммирующую машину, в которой использован принцип 10-зубых колес.

В 1969 году по чертежам Леонардо да Винчи  американская фирма IBM по производству компьютеров в целях рекламы построила работоспособную машину.

В Национальной библиотеке Мадрида были найдены неопубликованные рукописи Леонардо да Винчи. Среди чертежей был обнаружен эскиз 30-зарядного суммирующего устройства с десятизубыми колесами.